ADVERTISEMENT

Pharmacy Calculations for Pharmacy Technicians: Concentrations, Dilutions and Drug Dosing
INTRODUCTION
The primary goal of the profession of pharmacy is to improve public health through ensuring the safe and effective use of medications.1 The pursuit of this goal requires pharmacists and pharmacy technicians to achieve and maintain a wide range of knowledge and skills. For instance, those that have taken the Pharmacy Technician Certification exam understand that a substantial part of the exam is made up of questions that target medication order entry and the prescription filling process. This includes assessments of the candidate's ability to calculate individual drug doses and accurately convert between units of measurement. Thus, it is important for pharmacy technicians to have a fundamental understanding of everyday math problems that are commonly encountered in pharmacy practice. In the Pharmacy Calculations for Pharmacy Technicians: Units of Measurement and Methods of Calculation continuing education activity, the focal points included solving pharmacy math problems using dimensional analysis and ratio-proportion methods of calculation, converting between units of measurement, and determining the day's supply of medications. In Pharmacy Calculations for Pharmacy Technicians: Concentrations, Dilutions and Drug Dosing the focus is shifted to drug concentrations, dilutions, and individualized drug dosing. The goal of this activity is to ensure that doses of medications are appropriate for each individual patient. However, before new information is presented, a brief review of the dimensional analysis and ratio-proportion methods of calculation are presented. Conversions and abbreviations used in this activity are also provided below.
Common Conversions and Abbreviations
1000 mL = 1 L
1000 mg = 1 gm
2.54 cm = 1 inch
5 feet = 60 inches
2.2 lb = 1 kg
1 lb = 454 gm
Drop = gtt
Liter = L
Milliliter = mL
Gram = gm
Milligram = mg
Microgram = mcg
Kilogram = kg
Centimeter = cm
Pound = lb
Inch = in
DIMENSIONAL ANALYSIS AND RATIO-PROPORTION METHODS OF CALCULATION
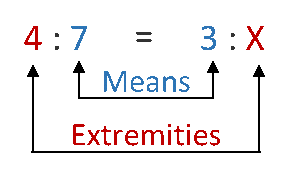
A ratio is the relationship between two numbers that are separated by a colon (e.g., 300:15). The ratio 300:15 is interpreted as 300 parts to 15 parts.2 Ratios are also written as fractions (e.g., 300/15). A proportion is an expression of two equal ratios and has the following two sets of values: means and extremities. When setting up a ratio-proportion calculation, two ratios are separated by an equal sign (=) or a double colon (::), such as 2 : 6 = 3 : X or 2 : 6 :: 3 : X. The inner values of the proportion, 6 and 3, are referred to as means, while the outer values, 2 and X, are referred to as extremities.2 When setting up proportion calculations, there will always be known and unknown variables. Importantly, three of the four variables in a ratio-proportion calculation must be known in order to solve for the unknown variable, which is typically represented by the letter X. Take, for instance, the following equation:
4 : 7 = 3 : X
Since three of the four variables are known, simply solve for the unknown variable X. This process is performed by multiplying the means (7 x 3) and extremities (4 x X) and solving for X. For example:
7 x 3 (means) = 4X (extremities) → 21 = 4X → X = 21 ÷ 4 = 5.25
Remember, ratios can also be set up as fractional equations. Take, for example, the previous proportion 4 : 7 = 3 : X. This equation can be set up using fractions and then solved by cross multiplication (see below).
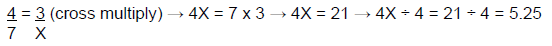
Dimensional analysis (DA) is another common method used to perform pharmacy math problems.
It involves the creation of a ratio-proportion pathway based on a combination of given quantities and known conversion factors within the metric and household systems of measurement.3 The following problem provides an example of when DA may be used in the pharmacy setting.

The pharmacy only has 250 mg tablets of azithromycin in stock. To dispense this prescription to the patient, the number of tablets needed for this dose needs to be calculated. In order to determine the correct number of tablets, you must know that 1 gram (g or gm) is equal to 1000 mg. Once this simple conversion has been performed, the DA equation can be set up in the following manner:
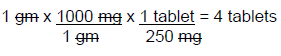
The calculation is performed by dividing the product of the numerators (1 x 1000 x 1 = 1000) by the product of the denominators (1 x 250 = 250), which equals 4 tablets. Remember, when developing the ratio-proportion pathway, it is important to establish units in the numerators and denominators that will cancel each other out through the process of cross cancellation, ultimately ending the calculation with the desired unit of measurement which in this case was tablets.
LIQUID AND SOLID DILUTIONS
Occasionally in pharmacy practice, a weaker solution must be made from a more concentrated solution such as a concentrated stock solution. These products are most often expressed in percent weight-volume (w/v) or percent weight-weight (w/w). Percent, as it relates to pharmacy, expresses the number of parts per 100. For example, a product expressed as 0.3% w/v is interpreted as 0.3 gm in 100 mL. Also, a product expressed as 10% w/w is interpreted as 10 gm in 100 gm. Many commercially available products are supplied with their concentration expressed in this format. Fluocinonide solution is one such product. It is supplied as a 0.05% solution, meaning that 100 ml of this product contains 0.05 g of fluocinonide. Another example would be 0.1% triamcinolone cream which has 0.1 gm of triamcinolone in every 100 gm of product. Situations sometimes occur when a needed strength is not in stock or the strength of a commercially available agent is not appropriate and a lower strength is required for a patient. This can be accomplished by combining the available product with an acceptable diluent.
When calculating liquid and solid dilutions, the following formula is useful and should be committed to memory2:
Q1 (quantity 1) × C1 (concentration 1) = Q2 (quantity 2) × C2 (concentration 2)
Examples using this mathematical formula for both liquid and solid dilutions are provided below.
Liquid dilution
Example: How many mLs of a 0.4% stock solution are required to make 2 L of a 0.06% solution, using water as the solvent? (1000 mL = 1 L)
In order to apply the above formula, three variables must be known. In this example problem, C1 (0.4%), Q2 (2 L), and C2 (0.06%) are known. The unknown variable which needs to be determined is Q1. To solve the problem, insert the numerical values into the formula and solve for Q1. It is important to remember that you should work with similar units while performing these calculations. In this case, the final answer is to be stated in mL; thus, 2 L should be converted to mL prior to using the formula.
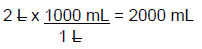
Q1 = ?
C1 = 0.4%
Q2 = 2000 mL
C2 = 0.06%
(Q1)(0.4%) = (2000 mL)(0.06%) → (Q1)(0.4%) = 120 → Q1 = 120 ÷ 0.4 = 300 mL
Therefore, 300 mL of a 0.4% stock solution is required to compound the liquid. Now, we must determine how many milliliters of solvent are necessary. To calculate the amount of solvent (water) to include in the compound, simply subtract the volume of the stock solution from the final volume of the compound.
2000 mL (final volume of the compound) - 300 mL (volume of stock solution) = 1700 mL of water
Thus, 300 mL of the 0.4% stock solution and 1700 mL of water (solvent) are required to make 2000 mL, or 2 L, of 0.06% solution. Let's try another problem involving liquid dilution. In the next example, the formula is used to find the concentration for a diluted solution.
Example: What is the new concentration of a 750 mL, 50% dextrose solution that is diluted to 1500 mL with water?
Q1 = 750
C1 = 50%
Q2 = 1500 mL
C2 = ?
(750 mL)(50%) = (1500 mL)(C2) → 37,500 = (1500 mL) (C2) → C2 = 37500 ÷ 1500 = 25%
By diluting 750 mL of a 50% dextrose solution to 1500 mL with water, the resulting concentration is dextrose 25%. Notice there is no change in the quantity of active ingredient, but we are doubling the volume; consequently, the concentration of the solution decreased by half.
The dilution of solid products, such as creams and ointments, follows the same rules. Solid products are typically diluted with ointments or bases that do not contain active drug. Let us look at an example of a solid dilution.
Solid dilution
Example: How many grams of a 5% lidocaine ointment and how many grams of an ointment base must be combined to obtain 3 pounds (lb) of 2% lidocaine ointment?
Remember that 1 lb = 454 gm. Use the same mathematical formula that was used in the liquid dilution examples listed above, Q1 × C1 = Q2 × C2.
Use DA to convert 3 pounds to grams →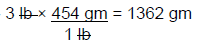
Q1 = ?
C1 = 5%
Q2 = 1362 gm
C2 = 2%
(Q1)(5%) = (1362 gm)(2%) → Q1 = 2724 ÷ 5 = 544.8 gm (rounded = 545 gm)
Therefore, 545 gm of 5% lidocaine ointment is required to compound the desired product. The next step is to determine how much of the base is needed. Since we know the final weight of the product (1362 gm) and the amount of 5% lidocaine ointment (545 gm) that is required, the amount of ointment base can be calculated.
1362 gm – 545 gm = 817 gm of ointment base
Let's look at another problem involving solid dilutions. Again, the next example will find the final concentration rather than the needed quantities.
Example: A 0.05% fluocinonide 30 gm ointment is combined with 15 gm of ointment base. What is the new percent strength? For this problem, two methods for finding the strength will be demonstrated.
The first example will use the concentration-quantity formula, Q1 × C1 = Q2 × C2:
Q1 = 30 gm
C1 = 0.05%
Q2 = 45 gm
C2 = ?
(30 gm)(0.05%) = (45 gm)(C2) (Note: 15 gm is added to 30 gm, resulting in 45 gm)
(30)(0.05) = (45)(X) → 1.5 = (45)(X) → 1.5 ÷ 45 = X → X = 0.03%
Therefore, the new percent strength of fluocinonide is 0.03%
The new percent strength can also be found using the ratio-proportion method. This approach is demonstrated below. The original concentration is 0.05%, meaning that there is 0.05 gm of fluocinonide in 100 gm of the ointment. Based on this information, how many grams of fluocinonide are in 30 gm?
Set up the following proportion then cross multiply:
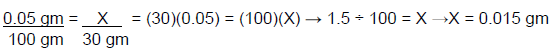
X = 0.015 gm, which means that 0.015 gm of fluocinonide are in a 30 gm tube. What is the percent strength of the product after adding 15 gm of ointment base (the amount of active ingredient remains the same, but the total weight increases to 45 gm)?
Thus, 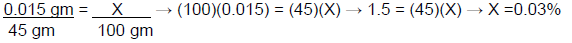
ALIQUOTS
In pharmacy practice, there are situations when a very small amount of drug is required. This presents a problem as measuring devices such as balances or graduated cylinders have a minimum weighable quantity (MWQ) or minimum measurable quantity (MMQ) that limits the amount that can accurately be weighed. For example, if a compound requires 20 mg of codeine and the available balance has a MWQ of 120 mg, the necessary amount would not be measurable. An aliquot can be used to obtain smaller than measurable amounts.4 Aliquot means containing an exact number of times in something else or when you divide the factor into the amount, there is no remainder.4 In pharmacy, the aliquot method refers to measuring out a small amount of a chemical or drug by diluting a larger amount, making the needed quantity measurable.5 An example is provided below.
Example: Prepare 100 mL of a 0.3 mg/mL clonidine solution using water as the diluent. First determine how much clonidine is needed.
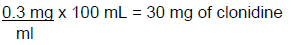
Assuming the MWQ for the balance available is 120 mg, 30 mg is not a measurable quantity. The aliquot method can be used. It is important that measurable quantities are selected without being so large that resources are wasted. Since we know that 120 mg can be measured, the calculation will be performed using 120 mg of clonidine. Because the aliquot also needs to be measurable, 5 ml will be selected as the volume of the aliquot. Therefore, because the needed amount of clonidine is 30 mg, the concentration of the aliquot will be 30 mg/5 mL. This can be performed as a proportion to determine the volume needed to dilute 120 mg of clonidine to a 30 mg/5 mL concentration.
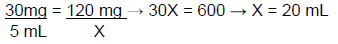
To obtain 30 mg of clonidine needed for this compound, the first step would be to dilute 120 mg of clonidine with 20 mL of water. Then, a 5 ml aliquot could be measured and then further diluted to the final volume of 100 mL. This calculation will work with solid dosage forms as well, using inert diluents such as lactose.
ALLIGATION
Alligation is a method that involves mixing similar solutions or solids to calculate a particular percent strength that is not available through a supplier or may not be on hand in the pharmacy. Figure 1 is an illustration that shows how alligation problems can be set up mathematically.
Figure 1.
Alligation Procedure

Importantly, in order to use this method, the desired strength (Box C) of the final product must be somewhere in between the two components that are being used (i.e., Box A and Box B).2,3,6 In other words, the concentration of the end product cannot be stronger than Box A or weaker than Box B. For example, if a physician writes an order for 500 mL of 12.5% dextrose in water and the pharmacy only has 50% dextrose in water and 5% dextrose in water in stock, the product can be compounded using these two products because 12.5%, the desired concentration, is between 50% and 5%.
In Figure 1 notice that the difference between the available concentrations and the desired concentration should be found in a diagonal fashion. Though subtracting the desired strength from the weakest component will result in a negative number, the number should be reported as positive to correctly perform this calculation.
Using the previous example:
A (Strongest component) = 50%
B (Weakest component) = 5%
C (Desired strength) = 12.5%
The calculation can be set up as demonstrated in Figure 2.
Figure 2

To determine the number of weakest parts (ie, dextrose 5%) that will be needed, the difference between Box A and Box C needs to be found (see Figure 3).
E = A - C = 50% - 12.5% = 37.5 parts
Figure 3
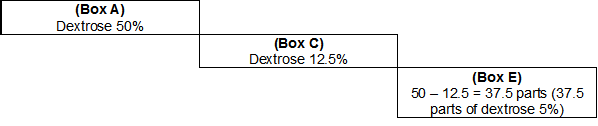
To find the number of parts of the stronger component, a similar method is used (see Figure 4). D = C – B = 12.5% - 5% = 7.5 parts
Figure 4

Now that the number of parts of the weaker component and the stronger component are known, the total number of parts, or Box F, can be found (see Figure 5).
F = D + E = 7.5 + 37.5 = 45
Figure 5

The number of total parts and the number of parts for each component have been found yet this is not the end of the calculations necessary to prepare this solution. The parts must be converted into a measurable amount based on the total volume required. In this case end volume should be 500 mL.
How much 50% dextrose (the stronger component) is required?
This amount can be found using several different methods. For this example, a ratio will be used.
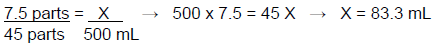
This can also be expressed as the number of 50% dextrose parts (7.5) divided by the number of total parts (45) then multiplied by the desired volume (500 mL), which provides the amount of 50% dextrose that is needed for the compound. This calculation is shown below.
(7.5 ÷ 45)(500 mL) = 83.3 mL of dextrose 50%
How much 5% (the weaker component) dextrose is required?
As above, this will be demonstrated using two methods. Using a ratio, the calculation would be:
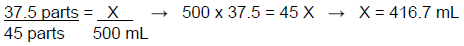
The second option would be to divide the number of 5% dextrose parts (37.5) by the number of total parts (45) and then multiply by the desired volume (500 mL), which provides the amount of 5% dextrose that is required for the compound. The calculation is shown below.
(37.5 ÷ 45)(500 mL) = 416.7 mL of dextrose 5%
As a final option, you could subtract the amount of the stronger component from the total to find the volume of the weaker component in mLs. Despite the method used, mixing 83.3 mL of 50% dextrose with 416.7 mL of 5% dextrose creates 500 mL of a 12.5% dextrose solution. Importantly, this product would be compounded by selecting a 500 mL bag of 5% dextrose, removing 83.3 mL, and adding 83.3 mL of 50% dextrose. It is common for pediatricians to order unique large- volume dextrose concentrations for neonates that are not readily available in premade IV bags; therefore, these calculations are practical and may often be needed in the hospital pharmacy setting.
Let's try another problem but with a w/w concentration.
Example: The pharmacy receives the following prescription

The pharmacy does not have this concentration of hydrocortisone in stock; however, 2.5% and 1% hydrocortisone products are available. Determine how much of each product is necessary to create 30 gm of a 1.5% hydrocortisone ointment. This is a possible solution because the desired concentration (1.5%) is between the available strengths (1% and 2.5%).
A (Strongest component) = 2.5%
B (Weakest component) = 1%
C (Desired strength) = 1.5%
The calculation is set up in Figure 6.
Figure 6

1.5% - 1% = 0.5 parts (Box D)
2.5% - 1.5% = 1 parts (Box E)
0.5 parts + 1 part = 1.5 parts (Box F)
Using the calculations outlines in the above figure, it was found that 0.5 parts of 2.5% hydrocortisone and 1 part 1% hydrocortisone will be used to make the final concentration of 1.5% hydrocortisone. Now, these numbers need to be converted to a measurable quantity, such as grams.
How much 2.5% hydrocortisone is required?
Using a ratio method:
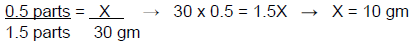
The number of 2.5% hydrocortisone parts (0.5) can also be divided by the total number of parts (1.5) and multiplied by the desired quantity (30 gm), which provides the amount of 2.5% hydrocortisone to be included in the compound (see below).
(0.5 ÷ 1.5)(30 gm) = 10 gm of 2.5% hydrocortisone
How much 1% hydrocortisone is required?
Using a ratio method:
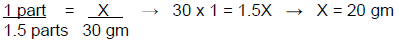
The number of 1% hydrocortisone parts (1) is divided by the total number of parts (1.5) and multiplied by the desired quantity (30 gm), which provides the amount of 1% hydrocortisone to be included in the compound (see below).
(1 ÷ 1.5)(30 gm) = 20 gm of 1% hydrocortisone
Therefore, mixing 10 gm of 2.5% hydrocortisone with 20 gm of 1% hydrocortisone creates 30 gm of a 1.5% (w/w) hydrocortisone ointment.
INDIVIDUALIZED DRUG DOSING
Ensuring appropriate dosing in an important component of pharmacy practice. To ensure safe, effective treatment for patients, a weight-based dosing method is often used for populations such as pediatric or elderly patients, and it is in the prescribing information for many medications.7 In healthcare, clinicians may also use body size descriptors such as ideal body weight (IBW), adjusted body weight (ABW), or body surface area (BSA) to dose drugs in patients at the extremes of body size to increase effectiveness and reduce toxicity.3,8 Specific dosing recommendations for medications can be found in printed references, a myriad of software applications, and product package inserts, which are typically referenced as milligrams per kilograms (mg/kg)—not milligrams per pound (mg/lb). Therefore, it is important that pharmacy technicians are aware that 1 kg is equal to 2.2 lb and can convent a patient’s weight from lb to kg or vice versa. Following is an example of how to accurately individualize drug dosing using actual body weight.
Example

For the above prescription, the patient weighs 30 lb. Calculate the correct dose and needed amount for the patient using actual body weight. The pharmacy has cefdinir 125mg/5ml available to dispense.
Step 1: Convert the patient's weight from lb to kg
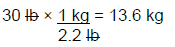
Step 2: Determine the total daily dosage
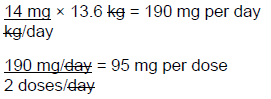
Step 3: After the dose is calculated, the next step is to calculate the amount of drug (in mL) required for each dose based on the concentration of the available cefdinir product (125 mg/5 mL). This problem can be solved using a variety of methods, including setting up a fractional equation, ratio-proportion, and DA. Let's solve using the ratio-proportion method.
125 mg : 5 mL = 95 mg : X (multiply the means and extremities and solve for X)
(5) (95) = (125)(X) → 475 = 125 X → 475 ÷ 125 = X → X = 3.8 mL
Therefore, the patient should be instructed to take 3.8 mL twice daily for a total of 7 days
Step 4: How many milliliters should be dispensed?
Dispense quantity sufficient
Solve by DA →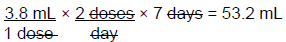
Therefore, a total of 53.2 mL of cefdinir is needed for this prescription. A 60 mL bottle is in stock. This product can be used with the instructions to discard the remaining amount after the 7 day course of therapy is complete.
Body Surface Area (BSA)
BSA is generally considered the most accurate method used to calculate drug doses because it is a mathematical function of height and weight.3 BSA is most often used when dosing chemotherapy drugs and can be calculated by the inches and pounds method or the metric formula that utilizes centimeters and kilograms. Below formulas that can be used to calculate a patient’s BSA. Note: the symbol (√) represents the square root function.
Inches and pounds formula3: BSA = √([ht(in) × wt(lb)] ÷ 3131)
Centimeters and kilograms formula3: BSA = √([ht(cm) × wt(kg)] ÷ 3600)
Example
BR is to receive IV cisplatin 50 mg/m² on day 1 of a 28-day cycle. BR weighs 160 lb and is 68 in tall. Calculate the correct dose for BR based on BSA.
Step 1: Based on the information provided in the above order, use the inches and pounds method for calculating BSA.
BSA = √([68 in × 160 lb] ÷ 3131) = 1.86 m²
BSA = 1.86 m²
Step 2: Calculate the correct dose for BR
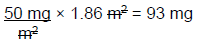
Therefore, BR should receive 93 mg of IV cisplatin on day 1 of a 28-day cycle.
The next example uses the metric system.
JM is a 24-year-old woman who is to receive IV liposomal doxorubicin 20 mg/m² on day 1 of a 21-day cycle. JM weighs 78 kg and is 165 cm tall.
Step 1: Based on the information provided in the above order, use the kg and cm calculation for determining BSA.
BSA = √([165 cm × 78 kg] ÷ 3600) = 1.89 m²
BSA = 1.89 m²
Step 2: Calculate the correct daily dose for JM
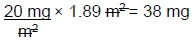
Therefore, JM should receive 38 mg of IV liposomal doxorubicin on day 1 of a 21-day cycle.
Ideal Body Weight (IBW)
Drug dosing by IBW is used for medications that are poorly absorbed and distributed throughout body fat, such as IV gentamicin and IV acyclovir.3 The most commonly used IBW calculation, the Devine Formula, is based on height; also, separate formulas exist for men and women (listed below).5 It is important for the correct IBW formula to be chosen for each patient because under- or overdosing of a medication may occur should the wrong equation be used.
Men: 50 kg + (2.3 kg x the number of inches over 5 feet)
Women: 45.5 kg + (2.3 kg x the number of inches over 5 feet)
Example: MB is a 27-year-old woman who weighs 71 kg and is 68 inches tall. What is MB's IBW?
Step 1: First, determine MB's height in inches and count the number of inches beyond 5 feet. Since 5 feet is = 60 inches, MT is 8 inches over 5 feet.
68 in – 60 in = 8 in
Step 2: Now, insert this value into the IBW formula for women.
45.5 kg + (2.3 kg x 8) = 45.5 kg + 18.4 kg = 63.9 kg
MB's IBW is 63.9 kg
The next example is for a male patient.
Example: JT is a 64-year-old man weighs 89 kg and is 75 inches tall. What is JT's IBW?
Step 1: Determine the number of inches JT is over 5 feet.
75 in – 60 in = 15 inches
Step 2: Now, insert this value into the IBW formula for men and calculate JT's IBW
50 kg + (2.3 kg x 15) = 50 kg + 34.5 kg = 84.5 kg
JT's IBW is 84.5 kg
The next example with demonstrate how IBW is used when calculating a dose for a patient.
Example: MT is a 38-year-old man who presents to the emergency room (ER) with the chief complaint of unrelenting fever for the past 24 hours. He indicates that he has been taking 650 mg of acetaminophen around the clock with no relief and that he does not take any other medications. After careful deliberation, the ER physician diagnoses MT with fever of unknown origin and elects to empirically treat for viral encephalitis. He orders acyclovir 30 mg/kg/day divided every 8 hours and requests the pharmacy to assist with dosing. MT's chart indicates that he weighs 180 lb and is 188 cm tall. Calculate MT's IBW and the correct acyclovir dosing regimen.
Step 1: Note that the patient’s height is reported in cm’s rather than inches in this case. To use the formula to calculate IBW the height must be converted to inches. It is important to remember that 1 inch = 2.54 cm
Use DA to determine MT's height in inches.
188 cm × 1 in = 74 inches
2.54 cm
Step 2: Calculate the number of inches MT is over 5 feet and insert that value into the correct IBW formula.
(74 inches – 60 inches) = 14 inches
50 kg + (2.3 kg x 14) = 50 kg + 32.2 kg = 82.2 kg
MT's IBW can be rounded to 82 kg. Since we now have MT's IBW, we can calculate his dosing regimen for IV acyclovir.
Step 3: Referring back to the original order from the physician, acyclovir was written as 30 mg/kg/day divided every 8 hours.
30 mg x 82 kg x 1 day = 2460 mg per day
kg
However, this is the total dose to be given over the course of 24 hours. Therefore, we must divide 2460 mg by 3 because MT is to be given in 3 separate doses over the course of 24 hours, spaced 8 hours apart:
2460 mg ÷ 3 = 820 mg
MT will receive 820 mg of IV acyclovir every 8 hours.
Adjusted Body Weight (ABW)
Adjusted body weight (ABW) is often used when dosing select medications in patients who are considered obese.3 The definition or cutoff for obesity varies by institution, although patients who have body fat contents greater than 25% to 30% of their actual body weight are generally considered obese.9 A common definition of extreme or morbid obesity is a weight that is greater than 200% of IBW.9 Following are 2 examples of ABW calculations9:
ABW = IBW + (0.4)(actual body weight – IBW)
ABW = IBW + (0.3)(actual body weight – IBW)
The most common drug class that is dosed using ABW includes antimicrobials that distribute well in water, but not in adipose tissue (i.e., gentamicin and tobramycin). These types of drugs are often referred to as polar or hydrophilic, meaning that they have a high affinity for water. The recommendation is to use an ABW when calculating dosages with these drugs (especially for obese patients) because dosing these medications according to IBW may result in suboptimal dosages. Adipose tissue does contain some water. However, in comparison it contains approximately 30% to 40% of what is found in other tissues.9 Due to this difference, obese patients who are dosed with polar antimicrobials will most likely require a dose increase that is proportional to their excess body weight. This dose increase is most often performed with the use of a correction factor, such as 0.4 or 0.3, which takes into account the water content of adipose tissue.9 These correction factors are shown in the above ABW equations.
Notably, the ABW formula is the same for both men and women; but the correction factor may vary, depending on the antibiotic that is used.9 Let's take a look at a few examples.
Example: CJ is a 23-year-old man who weighs 105 kg and is 70 inches tall. Calculate his ABW.
Step 1: First, calculate his IBW.
IBW = 50 kg + [(2.3 kg)(70 in – 60 in)] = 73 kg
Step 2: Now insert his IBW and actual body weight into the ABW formula.
ABW = 73 kg + [(0.4)(105 – 73)] → 73 kg + (0.4 x 32) = 73 kg + 12.8 = 85.8 kg
CJ's ABW = 85.8 kg. Notice, there is approximately a 13 kg or 29 lb difference between CJ's IBW and ABW, which can result in significant variations in drug doses.
Example: JR is a 45-year-old man who presents to the emergency department (ED) with altered mental status and pain during urination. After reviewing JR's labs, an ED physician diagnoses him with a urinary tract infection and orders a one-time dose of gentamicin before sending JR home. The order is written as follows: gentamicin 2 mg/kg IV x 1 dose, pharmacy to dose. JR is 317 lb and is 64 in tall. Calculate the correct dose for JR using the ABW formula.
Step 1: First, convert JR's weight from lb to kg.
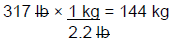
Step 2: Since we already know JR's height in inches (64), calculate his IBW.
50 kg + [(2.3 kg)(64 in – 60 in)] = 59.2 kg.
Step 3: Calculate JR's ABW using 0.4 as the correction factor.
59.2 kg + [(0.4)(144 kg – 59.2 kg)] = 93 kg
Step 4: Calculate the one-time dose of gentamicin, based on JR's ABW of 93 kg.
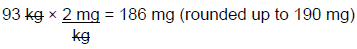
Therefore, JR should receive a 190 mg dose of IV gentamicin as a one-time dose in the ER.
IV DRIP RATES
In pharmacy, calculation of IV flow (drip) rates is sometimes necessary to ensure that patients are receiving the correct amount of medication ordered by the physician.10 Using flow rates you can calculate the volume of fluid or amount of drug a patient will be receiving over a certain period of time.10 Though programmable IV pumps are used in many clinical settings, it is important to understand this calculation. The rate can be found using dimensional analysis. Rates may be presented as mL per minute or drops (gtts) per minute. Providers may order IV medication as the amount of drug in mg, mcg, or units to administer per minute or hour.11 These rates require steps to determine the volume to deliver per unit of time. In the hospital setting, it may be necessary to determine the drip rate based on this information or the volume needed to supply a patient with the necessary amount of medication or fluid. In the course of their duties, pharmacy technicians in hospitals may be required to verify drip rate doses for patient safety, to enhance patient care, and to minimize drug waste.10 Examples are provided below.
Example: A physician orders diltiazem 100 mg/100 ml in normal saline to be infused at a rate of 5 mg/hour following a bolus dose. What rate would deliver the correct dose to the patient in mL per minute?
Step 1: First, the rate given needs to be converted from mg to mL, based on the concentration from the order (100 mg/100 mL). This can be found using several methods. For this example, a ratio will be used.
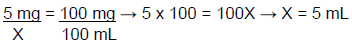
The patient needs 5 mL of diltiazem 100 mg/100 ml in normal saline per hour.
Step 2: Now the rate (5 mL/hour) needs to be converted to mL/min.
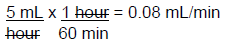
Occasionally, the rate may be needed in drops per minute. The following equation can be used if this type of rate needs to be found.ATI
Volume (mL) x drop factor (gtt/ml) = IV drip rate (gtt/min)
Time (min)
In this equation, the drop factor is the number of drops per mL based on the IV tubing used.
Example: A provider orders 1 L of 0.9% sodium chloride to infuse over 8 hours. You have macrodrip tubing with a drop factor of 15 gtt/mL. You must calculate the rate in gtt/min to set the IV flow rate.
Step 1: Convert the volume of the liquid to be infused from L to mL (1L = 1000 mL).
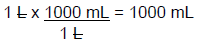
Step 2: Next, convert the time from hours to minutes.
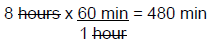
Step 3: Then, use the equation above to solve for the IV drip rate. The drop factor in the example given was 15 gtt/mL.
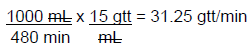
The rate can be rounded to 31 gtt/min. This multi-step calculation can be set up as one problem, making sure that the units counsel to leave the final units of gtt/min. This would begin with the rate in L/hour from the original order.
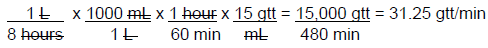
Another calculation related to drip rates is to determine the total volume that is needed for a patient to deliver the required amount of a drug or to last for a specific amount of time.
Example: An order is written for normal saline to be infused at a rate of 100 mL/hour over 8 hours. What volume will be needed for this patient?
Step 1: For this calculation, simply multiply the rate by the amount of time, making sure that the units cancel to leave you with volume.

CONCLUSION
One of the most important areas of study for a pharmacy technician is pharmacy calculations. Pharmacy technicians must be capable of performing a variety of calculations to effectively contribute to the daily practice of pharmacy, including dilutions, conversions between units of measurement, and a day's supply of medications. These calculations should always be checked and/or verified by another individual. Moreover, an increasing number of State Boards of Pharmacy have recognized the integral role of pharmacy technicians and have revised practice regulations to allow an increase in their responsibilities.1 For example, pharmacy technicians assist pharmacists with the technical aspects of dispensing prescriptions, such as computer order entry and medication preparation, which requires a firm understanding of pharmaceutical calculations.1 As new opportunities for pharmacy technicians continue to emerge, post-licensure credentials, education, and training are likely to expand to ensure the competence of all pharmacy technicians and to support their continuing professional development.1,12 One specific area of study in which pharmacy technicians must remain proficient is everyday pharmacy math problems, considering an error in a dosage calculation or dilution can pose significant harm to a patient.
REFERENCES
- Council on Credentialing in Pharmacy. Albanese NP, Rouse MJ. Scope of contemporary pharmacy practice: roles, responsibilities, and functions of pharmacists and pharmacy technicians. J Am Pharm Assoc. (2003). 2010;50(2):e35-e69.
- Zentz LC. Math for Pharmacy Technicians. Sudbury, MA: Jones and Bartlett Publishers, LLC; 2010.
- Kee JL, Marshall SM. Clinical Calculations with Applications to General and Specialty Areas. 7th ed. St. Louis, MO: Elsevier; 2013.
- 10 Aliquot Calculations. Basicmedicl Key website. June1, 2016. https://basicmedicalkey.com/10-aliquot-calculations/. Accessed July 2019.
- Bank E. How to Calculate Aliquot. Sciencing website. April 24, 2017. http://sciencing.com/calculate-aliquot-7257845.html. Accessed July 2019.
- Ansel HC, Stoklosa MJ. Pharmaceutical Calculations. 11th ed. Philadelphia, PA: Lippincott Williams &Wilkins; 2001.
- Pan SD, Zhu LL, Chen M, et al. Weight-based dosing in medication use: what should we know? Patient Prefer Adherence. 2016;10:549-560.
- Pai MP. Drug dosing based on weight and body surface area: mathematical assumptions and limitations in obese adults. Pharmacotherapy. 2012;32(9):856-868.
- Wurtz R, Itokazu G, Rodvold K. Antimicrobial dosing in obese patients. Clin Infect Dis. 1997;25(1):112-118.
- Philip Trapskin P, Reagan R, Hite K, Armitstead J. Pharmacy Calculations. April 2005. University of Kentucky Healthcare Pharmacy Services website. www.hosp.uky.edu/Pharmacy /resources/USP797/Pharmacy%20Calculations.ppt. Accessed July 2019.
- Calculating Intravenous Flow Rates. ATI Nursing Education website. http://www.atitesting.com/ati_next_gen/skillsmodules/content/medication-administration-4/equipment/IV-med-calculations.html. Accessed July 2019.
- Dussault G, Dubois C-A (BioMed Central Ltd). Commentary: Human resources for health policies: a critical component to health policies. Published April 14, 2003. Human Resources for Health Web site. http://www.human-resources-health.com/content/pdf/1478-4491-1-1.pdf. Accessed July 2019.
Back to Top