Shopping Cart

Introduction

The health care system in the United States (U.S.) is multifaceted and faces many unique challenges. A number of recent studies have identified that human and economic resources within the health care system are strained and not efficiently utilized,¹ emphasizing the need to make best use of the knowledge and skills that health care professionals acquire through education and training. With that in mind, pharmacy technicians are now taking on additional, more advanced, responsibilities, including some of those traditionally performed by pharmacists.² These roles include medication order entry, multiple-point checking, physically separating look-alike and sound-alike medications, and assisting pharmacists by collecting patient-specific data.³ One important element of pharmacy practice in which technicians play a key role is making sure that the right patient receives the right drug at the right dose. To maintain overall medication safety, there are several calculations that pharmacy technicians must be able to perform proficiently. The following provides a review of pharmacy calculations, aimed at increasing the technician's ability to solve everyday math problems as they relate to practical pharmacy situations.

NUMBER SYSTEMS REVIEW

There are many mathematic and scientific symbols that represent relative values or provide instructions for a specific calculation. With regard to the fundamentals of measurement and calculation in pharmacy practice, there are two number systems with which pharmacy technicians must be familiar—the Arabic system and Roman numerals. The Arabic system, properly called the decimal system, consists of only 10 numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and is the most commonly used system today.⁴ These numbers can be written as whole numbers, fractions, or decimals. Conversely, the Roman system uses letters in place of numbers; thus, it is of no use in computation. The Roman system is rarely used in practice, but may appear on prescriptions to communicate the desired quantity of medication to be administered (e.g., teaspoonfuls ii) or dispensed (e.g., capsules No. XXIV). When expressing quantities in the Roman system, 8 letters that represent fixed values are used, which are listed in Table 1.

Table 1. The Roman Numeral System5
Roman Numeral	Arabic Number
ss	1/2
I or i	1
V or v	5
X or x	10
L or l	50
C or c	100
D or d	500
M or m	1000

Roman numeral quantities, other than those listed in Table 1, may be expressed; but there are several rules that must be taken into consideration, which are listed below⁵:

1. If the first Roman numeral is equal to or greater than the numeral(s) that follow it, then the numerals are added together (i.e., the sum of their values). See Figure 1.

2. If a smaller Roman numeral is placed before a numeral of larger value, the smaller numeral is subtracted from the larger numeral (Figure 2).

3. When there are three or more numerals and a smaller numeral is placed between two Roman numerals of larger value, the smaller numeral is subtracted from the larger numeral that follows it (Figure 3).

FRACTIONS

Pharmacy calculations often require the use of common fractions. Fractions are expressed as part(s) of a whole and are composed of 2 basic numbers, a numerator (top number) and a denominator (bottom number).⁵ See Figure 4.

The above fraction, 2/3, may be converted to a decimal (or a number less than 1) by dividing the numerator by the denominator. For example, 2 ÷ 3 = 0.667. Notably, as the denominator (bottom number) of a fraction increases, the value of the fraction (or the number value) decreases because it takes more parts to make a whole (see below). For example, if you compare ½ to ¼, ½ is larger (e.g., ½ = 0.5 = 2 parts; ¼ = 0.25 = 4 parts, the latter being a smaller value). See Figure 5.

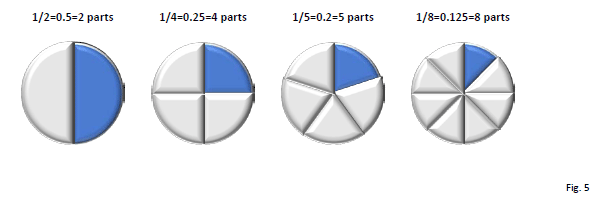
Following are the three primary types of fractions⁶:

1. A proper fraction is a fraction that has a numerator that is smaller than the denominator. For example, 3/5 is a proper fraction.

2. An improper fraction is a fraction where the numerator is larger than the denominator. For example, 4/3 is an improper fraction. When the numerator is divided by the denominator, the answer includes a whole number and a fraction. For instance, 4/3 = 4 ÷ 3 = 1 & 1/3 because 3 can be divided into 4 one time with 1 left over, or 1/3. This is referred to as a mixed number or a mixed fraction.

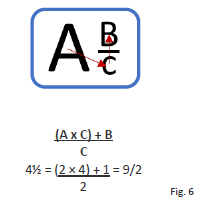
3. As previously mentioned, a mixed fraction is a fraction that includes a whole number and an additional fraction. To use a mixed fraction in a calculation, it must to be reduced to an improper fraction. To perform this calculation, you multiply the denominator by the whole number and add the numerator to that product; the final answer is then placed over the original denominator.⁶ An example is provided below.

Adding and Subtracting Fractions

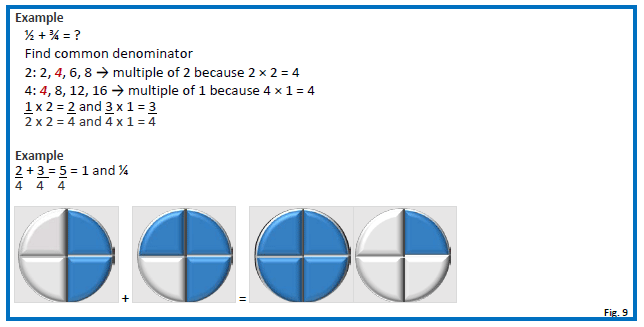
Adding and subtracting fractions requires a few steps to arrive at the correct answer. To add or subtract fractions, there must be a common denominator between fractions. Please take a look at the following example (Figure 7):

Since the denominators for each fraction are the same (the number 7), the numerator of each fraction can simply be added together while placing them over the existing denominator (answer = 4/7). Occasionally, fractions do not have a common denominator and the math problem will involve extra steps, as illustrated below (Figure 8).

To accurately complete a calculation where the denominators are not the same, the lowest common denominator must be determined. This can be done by listing multiples of each denominator until a common multiple is found. For instance, when you list multiples of each denominator from the above fractions, the first multiple that these fractions share is 21 (shown below).

3: 3, 6, 9, 12, 15, 18, 21, 24, 27 → multiple of 7 because 3 × 7 = 21
7: 7, 14, 21, 28, 35 → multiple of 3 because 7 × 3 = 21

The next step is to create new fractions that share this common denominator. This is performed by multiplying the numerator and denominator of each fraction by the multiples determined in the previous step (shown below).

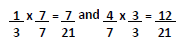
The new equation should look like this: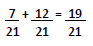

Remember, to accurately add or subtract fractions, the lowest common denominator must be established to solve the math problem. See Figure 9.

Multiplying Fractions

When multiplying fractions, multiply the numerators and then the denominators—a common denominator does not need to be determined. Whenever possible, reduce fractions to their lowest terms.

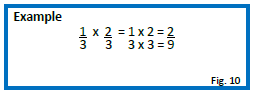
Dividing Fractions

When dividing fractions, invert the divisor (or second fraction) and then multiply the fractions as previously described. Whenever possible, reduce fractions to their lowest terms. In the following example, the divisor is highlighted in red (Figure 11).

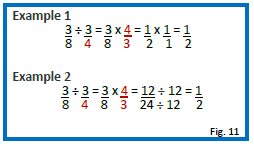
Notice the fraction 3/4 (divisor) was inverted to 4/3 and then the fractions were multiplied. In the first example, when reducing fractions to their lowest terms, the process of cross canceling is utilized. For instance, in the above example, the number 3 goes into both the numerator of the first fraction and the denominator of the inverted divisor 1 time. Secondly, the number 4 goes into the denominator of the first fraction 2 times and the numerator of the inverted divisor 1 time, resulting in the answer 1/2. Cross canceling is helpful because it allows you to work with smaller values. The second example does not use cross canceling. The answer 12/24 can be reduced to ½ because both the numerator and the denominator can be divided by 12.

DECIMALS

Decimals consist of whole numbers (numbers to the left of the decimal) and decimal fractions (numbers that are less than the whole number 1, which appear to the right of the decimal).⁵ For example, in the number 7.63, 7 is a whole number (left of the decimal) and 0.63 is a decimal fraction because it is less than the whole number 1 and is positioned to the right of the decimal. Decimal fractions are written in tenths (0.1 or 1/10), hundredths (0.01 or 1/100), thousandths (0.001 or 1/1000), ten-thousandths (0.0001 or 1/10,000), and so on.⁵ Decimals are important in pharmacy practice for the following two primary reasons: they are used often in the dosing of medications and many drugs are expressed in decimal fractions (e.g., digoxin 0.25 mg and levothyroxine 0.088 mg). Notably, when a decimal is changed to a fraction, the denominator is based on the number of units that appears to the right of the decimal (e.g., 0.93 = 93/100).⁵ The following examples further illustrate this point (Figures 12 and 13):

 

To effectively avoid medication errors involving decimals, some important rules for standard pharmacy practice must be in place. The Institute for Safe Medication Practices (ISMP) is a nonprofit organization that provides resources and information to help healthcare practitioners in a variety of healthcare settings prevent errors and ensure that medications are used safely.⁷ The ISMP has compiled a list of abbreviations, symbols, and dose designations that are often misinterpreted and can lead to medication errors. Recommendations for decimals are included in this list because misinterpretation can lead to patient harm. First, it is important to avoid the inclusion of trailing zeroes after the decimal point.⁸ For example, if a 1 mg warfarin dose is written as 1.0 mg (trailing zero), it may be interpreted as 10 mg, which would lead to a 10-fold dose increase, placing the patient at significant risk of bleeding. Conversely, the omission of a leading zero before the decimal, a "naked" decimal, can lead to medication errors as well. For instance, if warfarin 0.5 mg (one-half of a 1 mg tablet) is written as .5 mg, a 10-fold increase in the warfarin dose could occur if the decimal goes unnoticed and the prescription is interpreted as 5 mg. The appropriate use of the decimal point is critical to ensure patient safety. This concept is further illustrated below (Figure 14):

The complete list of abbreviations, symbols, and dose designations can be found at: http://www.ismp.org/tools/errorproneabbreviations.pdf⁸

Rounding

In many situations, it is necessary to round a number for consistency or for purposes of measurement. There are two simple rules for rounding:

1. Round up if the number following is 5 or greater
2. Round down if the number following is 4 or less

When rounding to a whole number, refer to the number after the decimal point. See Figure 15 for examples.

Rounding is useful when determining a dose for a patient based on the measuring devices that are available. For example, when dosing liquid medication it is important to know the size of the measuring device and the smallest measurable amount. Consider the following prescription:

For a patient who weight 38 lb, the amount per dose would be 2.42 ml. Most measuring spoons or syringes that are available would not be capable of measuring this amount. Depending on the demarcation of the device, the dose could be rounded to 2.4 mL or the prescriber may decide to use 2.5 mL (½ teaspoon) because it is easily measured. Instructing a patient or caregiver to measure 2.42 mL would not be practical in most situations.

The most common decimal calculations that occur in pharmacy practice involve addition, subtraction, and multiplication. The addition and subtraction of decimals is fairly straightforward—simply line up the decimals and add or subtract. It is important to note that for a whole number, the decimal appears to the right of the whole number. Zeros may need to be added as placeholders to add or subtract whole numbers and decimals. For example, the number 18 may be written as 18.0, 18.00, or 18.000, depending on the number of decimal places that are needed for a particular math problem. The value of 18 will not change no matter how many zeroes are added after the decimal. The example below (Figure 16) further highlights the concept of lining up decimals for addition and subtraction.

When multiplying decimals, the process is slightly different than addition and subtraction. Before multiplying, it is important to determine the number of decimal places that will be included in the final answer or product. This is performed by adding the number of decimal places in both numbers that are being multiplied. Once the total number of decimal places has been determined, the factors are then multiplied. After the final product has been determined, mark off the number of decimal places (from right to left) according to the total number of decimal places that were determined at the beginning of the calculation. Answers are typically rounded to the nearest tenths place. Take, for instance, the following example (Figure 17):

Four numbers appear after decimal points in the above problem. Thus, in the final product, the decimal is moved 4 places, from right to left, in order to arrive at the product 6.3063.

RATIO AND PROPORTION, FRACTIONAL EQUATIONS, AND DIMENSIONAL ANALYSIS

A ratio is the relationship between 2 numbers and is separated by a colon (e.g., 250:5). Ratios are also written as fractions (e.g., 250/5). The ratio 250:5 is interpreted as 250 parts to 5 parts. Moreover, a proportion is an expression of two equal ratios and has the following two sets of values: means and extremities.⁶ All three are very useful and commonly used in pharmacy practice. When setting up a ratio-proportion calculation, two ratios are separated by an equal sign (=) or a double colon (::), such as 1 : 4 = 2 : X or 1 : 4 :: 2 : X.⁶ The inner values of the proportion, 4 and 2, are referred to as means, while the outer values, 1 and X, are referred to as extremities.⁶ Importantly, when setting up proportion calculations, there will always be known and unknown variables. Three of the four variables in a ratio-proportion calculation must be known in order to solve for the unknown variable, which is often represented by the letter X. Take, for instance, the following equation:

2 : 3 = 4 : X

Notice that three of the four variables are already known and you are left with only one unknown. This math problem can be solved by multiplying the two means (3 x 4, which are the inner values) and then multiplying the two extremities (2 × X, which are the outer values) and solving for the unknown variable (X), as shown below.

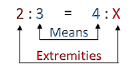
A ratio-proportion calculation can also be set up as a fractional equation. For instance, take the following example (Figure 19):

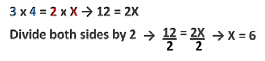
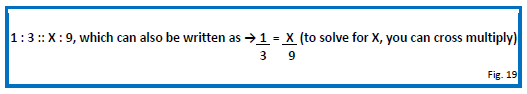
The above fractional expression is solved by the processes of cross multiplication and division to determine the value for the unknown variable X (see below).

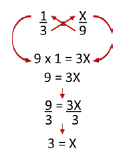
In addition to solving pharmacy math problems by ratio-proportion and fractional equations, dimensional analysis (DA) may be utilized. DA involves the creation of a series of proportions, based on a combination of given quantities in the particular math problem and known conversion factors within the metric and household systems of measurement. There are a few basic steps to follow when solving a pharmacy math problem by DA^4,5,6:

1. Determine the desired units for the final product
2. Determine the given quantities and their units of measurement
3. Determine the conversion factors that are to be included in the DA equation to arrive at the appropriately labeled (units) product
4. Proportions must be set up so that that the units in each numerator and denominator cancel each other out, leaving the desired units in the final step of the calculation
5. The calculation is performed by dividing the product of the numerators by the product of the denominators

A basic and frequently used example of DA involves unit conversions within the metric or household systems of measurement. For example, a provider wrote the following prescription for a pediatric patient who weighs 15 kg:

After verifying that this dose is appropriate for the patient, the next step is to calculate how much of the available suspension is needed for each dose. If using DA, the math problem would be set up in the following manner:

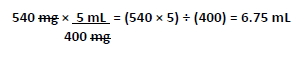
The patient would take 6.75 mL twice daily for 7 days. The DA equation begins with the known dose for the patient (540 mg) and the known concentration of the amoxicillin suspension (400 mg per 5 mL). Notice the concentration of the suspension has been inverted in the above equation, which allows for cross canceling of mg units. These cancellations result in the desired end unit(s), mL, which is included in the final answer (6.75 mL). When performing DA, it is important to set up proportions that allow for units to be cross canceled, in order to end the analysis with the desired unit of measurement. Finally, the answer should be rounded based on the amount measurable with the available dosing device. See below (Figure 21) for an additional example.

Note that the proportions were set up in such a way that units cancel as we work through the problem, so that the desired units (mL) appear at the end of the DA. The dose is converted from gm to mg first. To arrive at the final answer, the product of the numerators is divided by the product of the denominators, as shown in the above calculation. Other examples are provided below (Figure 22).

PERCENT CONCENTRATION

The term percent and its corresponding sign (%) is defined as"of each hundred".⁴ Percent concentrations of pharmaceutical preparations generally fall into one of the following three categories⁴:

1. Percent weight-in-volume (w/v) expresses the number of grams of a constituent in 100 mL of a solution. For example, 0.9% NaCl means 0.9 gm of sodium chloride is in every 100 mL of the solution (Figure 23).

2. Percent volume-in-volume (v/v) expresses the number of milliliters of a constituent in 100 mL of a particular solution. For example, 4% liquid phenol means that 4 mL of liquid phenol are in every 100 mL of solution (Figure 24).

3. Percent weight-in-weight (w/w) expresses the number of grams of a constituent in 100 grams of a preparation. For example, 1% hydrocortisone cream means that 1 gram of hydrocortisone is in every 100 grams of the preparation (Figure 25).

MEASUREMENT SYSTEMS

It is critical that pharmacy technicians understand systems of measurement. The two systems of measurement that are most commonly used in pharmacy practice today are the metric and household systems⁵; however, technicians should also be aware of both the avoirdupois and apothecary units of measurement. Table 2 lists common unit equivalents of each of the above-mentioned systems of measurement. The avoirdupois system is the common system of commerce (along with the metric system) in the U.S. for items that are purchased and sold by the ounce or pound.⁴ Conversely, the apothecary system originated in Ancient Greece, which uses grains, scruples, and drams as units of measurement for weight and volume.⁴ However, both systems have predominantly been replaced by the metric system. Still, prescriptions are occasionally written using apothecary units of measurement (e.g., Nature Throid or WP Thyroid; 1 grain = 65 mg), emphasizing the need for pharmacy technicians to have a working knowledge of each system of measurement in order to accurately prepare medications, in addition to explaining dosing instructions to patients and caregivers.

Table 2. Systems of Measurement5,6,7
Metric System
Weight	Volume
1 kilogram (kg) = 1000 grams	1 Liter (L) = 1000 milliliters
1 gram (gm) = 1000 milligrams	1 deciliter (dL) = 100 milliliters
1 milligram (mg) = 1000 micrograms	1000 milliliters (mL) = 1 liter
Apothecary System
Weight	Volume
1 grain (gr) = 65 mg	1 fluid dram (fl dr) = 5 mL
60 grains (gr) = 1 dram	8 fluid drams (fl dr) = 1 fluid ounce
8 drams (dr) = 1 ounce	16 fluid ounces (fl oz) = 1 pint
12 ounces (oz) = 1 pound	4 quarts (qt) = 1 gallon
Avoirdupois System
Weight	Volume
1 ounce (oz) = 437½ grains	8 ounces (oz) = 1 cup
1 pound (lb) = 16 ounces	2 cups (c) = 1 pint
16 ounces (oz) = 7000 grains	2 pints (pt) = 1 quart
Household System
1 tablespoon (tbsp) = 15 milliliters 2 tablespoon (tbsp) = 1 ounce or 30 mL
1 teaspoon (tsp) = 5 milliliters
1 pint (pt) = 16 fluid ounces or 473 mL
1 cup (c) = 8 ounces
1 fluid ounce (fl oz) = 29.57 mL or 30 mL

The metric system is a decimal system based on multiples and divisions of 10. The three basic units of measurement in the metric system include the following⁵:

1. Gram (g, gm): unit for weight
2. Liter (L, l): unit for volume
3. Meter (M, m): unit for length

Prefixes are attached to root words, which represent the standard units of measure, to indicate whether numbers are larger or smaller than these basic units of measurement (e. g., milligram = 0.001 or one-thousandth of a gram or 1000 mg = 1 gm).⁵ Pharmacy calculations frequently require conversions within the metric system to prepare correct dosages of medications. Most drug doses are provided in grams, milligrams, or micrograms, while liquid formulations and solutions are typically expressed in milliliters or liters. When converting between metric weights and volume, there are 2 rules to commit to memory whether converting from smaller to larger or from larger to smaller units of measurement.

Rule Number 1 : Divide when going from a smaller to a larger unit of measurement.⁵ For example, if a calculation calls for the conversion of 500 milliliters to liters, you would have to divide 500 milliliters by 1000, because there are 1000 milliliters in 1 liter (see below). This conversion has been performed below using DA (Figure 26).

Rule Number 2: Multiply when going from a larger to a smaller unit of measurement.⁵ For example, if a calculation calls for the conversion of 2 grams to milligrams, you would have to multiply 2 grams by 1000, because there are 1000 mg in 1 gram (see below). The conversion has been performed below using DA (Figure 27).

It is also important to understand the conversion processes between metric and household units of measurement because household units often appear on prescriptions for suspensions or elixirs; many patients are familiar with this system of measurement. The following will serve as an example:

The patient wants to know how many teaspoons are in 30 mL. This math problem can be solved by using DA, ratio-proportion, or setting up a fractional equation (shown below). In order to perform this calculation, you must be aware that 1 teaspoon = 5 mL. This basic conversion is used frequently in the pharmacy setting and should be committed to memory.

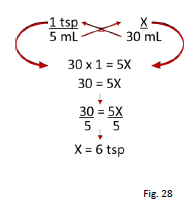
Since we know that 1 teaspoon is equal to 5 mL and the prescribed dose is 30 mL, three variables are known. Therefore, proportions can be set up to solve for the unknown variable X. Note: it is important to keep the units on each side of the equation in the same order, as shown in the above example (i.e., teaspoons are expressed in the numerator of each ratio and milliliters are expressed in the denominator of each ratio).

OR, the above problem can be solved using the ratio-proportion method:

mL : tsp (of the known) :: mL : tsp (of the desired)

5 mL : 1 tsp :: 30 mL : X tsp → multiply the means and extremities as shown below

30 × 1 :: 5 × X → 30 = 5X → X = 30 ÷ 5 = 6 tsp

CALCULATING DAY'S SUPPLY

One the most common calculations that is performed in community pharmacy practice is finding the day's supply of a medication. A fundamental understanding of this calculation is essential for insurance purposes as errors could result in incorrect reimbursement, claim rejections, or audit "red flags".⁹ It is also important when counseling patients about the expiration of products, such as antibiotic suspensions. While many drugs are dosed once daily, some medications should be taken more often. For instance, dosing instructions on some prescriptions may call for medications to be taken two to four times daily (e.g., commonly written by providers as BID and QID, respectively), which will impact the amount of medication necessary for a 30- or 90-day supply. Therefore, it is important that pharmacy technicians pay close attention to the dosing instructions on each individual prescription. For oral solids, including tablets and capsules, the day's supply calculation is fairly straightforward—if a patient is taking metformin 500 mg twice daily, dividing the quantity prescriber by the number of doses taken per day would give you the day's supply. Thus, #60 metformin 500 mg tablets would last this patient 30 days. When dosing regimens become more complicated, determining the day's supply can become more complex. Consider the following prescription:

To calculate the day's supply for this prescription, you must determine the maximum number of tablets that the patient can take during one day. Divide the number of hours in one day by how often the dose can be taken.

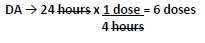
In this situation, one dose is one tablet so 6 doses equals 6 tablets. The next step is to divide the quantity prescribed by the maximum number of doses allowed per day. DA can also be used here, making sure that units cancel.

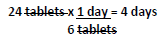
This calculation often needs to be performed for liquid dosage forms. Because the dose is most often written for teaspoons or milliliters, the amount per dose must be considered to determine the day's supply. How would the previous example differ if the promethazine solution were prescribed?

Note in this example that an extra step was required to find the maximum amount of solution that the patient is prescribed per day (Figure 30).

Similarly, it is important to be able to calculate how much medication a patient will need to complete a course of therapy. Liquid formulations, such as antibiotic suspensions, often require dispensing reconstituted bottles with more medication than the actual quantity written on the prescription. In these situations, it is important that the patient or caregiver is counseled to discard the remaining contents of the bottle after the entire course of therapy has been completed. Consider the following prescription for a 9-year-old child weighing 35 kg:

The medication is available in 15 ml, 22.5 ml, and 30 mL bottles. How would you calculate the correct dose in mL and determine the size needed for the patient to complete the course of therapy (Figure 31)? After looking up the dose, you see that the dose is appropriate for this patient because the reference indicates the following: 10 mg/kg on day 1, then 5 mg/kg every 24 hours for 4 consecutive days.

Calculating day's supply can be challenging for ophthalmic and otic preparations. For these liquid solutions and suspensions for the ear and the eye, the number of drops in each mL must be known to ensure that the day's supply is correct and that the patient is given enough product to complete their recommended treatment. The standard conversion factor is 20 drops per mL.⁹ Examine the following prescription and example for calculating day's supply (Figure 32):

Other potentially problematic dosage forms and recommendations for calculating day's supply are listed below.⁹

Inhaled products: Calculate the total number of actuations or doses to be dispensed by multiplying the number of actuations or doses per inhaler by the number of inhalers to be dispensed Then divide the total number of actuations or doses to be dispensed by the number of actuations or doses used per day.

Vaginal products: Consider the dosing interval between the insertion of the vaginal product, and the number of days that must elapse before insertions of a new product.

Topical products: Consider the frequency and size of the area treated. Generally, each gram of product will cover an area represented by four handprints.

Putting Knowledge to Practice: Sample Calculations

Problem 1

Due to a drug shortage, a hospital is out of 1 liter bags of D5½NS, although they have an abundance of 1 liter bags of ½NS. It is decided that instead of borrowing IV fluids from a nearby hospital, the pharmacy staff will compound D5½NS with 1 liter bags of ½NS and vials of dextrose. How many grams of dextrose should be added to a one liter bag of the available solution (½NS) in order to make the needed product (D5½NS)?

D5 or D5W is an acronym commonly used in place of 5% dextrose in water. Recall that percent w/v means the number of grams of a constituent in 100 mL of fluid. Thus, D5W equates to 5 grams of dextrose in 100 mL of water. NS is an abbreviation for normal saline, or 0.9% sodium chloride in water. Half normal saline, ½ NS, is half of the strength of normal saline, or 0.45%. For this problem, since we know the percent w/v, we can set up a proportion, DA, or fractional equation to determine how many grams of D5W will be necessary to add to a 1 liter bag of ½NS to make D5½NS (below).

1. As w/v percent concentrations involve grams per mL, we need to convert L to mL so we are working with common units of measurement, which can be performed by using DA.
   • 
     
     
2. Since 3 variables are known (5 gm dextrose per 100 mL, and 1000 mL), you can set up the following proportions: 5 gm : 100 mL :: X : 1000 mL
   • Remember, keep the units in the same order and multiply the means (inner values) and the extremities (the outer values), and then solve for X
   • (100 × X) = (1000 x 5) → (100)(X) = (5000) → X = 5000 ÷ 100 = 50 gm dextrose
     
     
3. Thus, 50 grams of dextrose should be added to the 1 liter bag of ½NS to make D5½NS.

However, the hospital only has 50 mL vials of 50% dextrose available for the IV compound. How many vials of 50% dextrose will have to be added to the bag?

1. Recall from the above calculation that percent w/v equates to grams of constituent per 100 mL. Thus, 50% dextrose means 50 gm of dextrose per 100 mL of fluid or solution. However, since the vial is only 50 mL and not 100 mL, we must determine how many grams of dextrose are in the vial.
2. Use 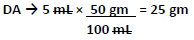of dextrose are in each 50 mL vial
   
   
3. Now, set up a proportion to determine the number of vials needed to add to the IV solution. Recall from the first part of this math problem that we have already determined that 50 grams of dextrose must be added to the 1 L bag of ½NS to make D5½NS. Therefore
   • 25 gm : 1 vial :: 50 gm : X vials
   • (1 × 50) = (25)(X) → (50) = (25)(X) → X = 50 ÷ 25 = 2 vials
4. Therefore, 2 vials of 50% dextrose (50 mL) are needed to compound the IV fluid.

Problem 2

How many grams of hydrocortisone are in 4 grams of 0.2% hydrocortisone valerate ointment?

1. Recall the percent strength w/w equates to the number of grams of a constituent in 100 grams of a preparation (i.e., cream, ointment). Therefore, 0.2% hydrocortisone means 0.2 gm of hydrocortisone is in 100 gm of ointment.
2. Now there are enough variables set up a fractional equation or proportion (4 gm, and 0.2 gm per 100 gm). Remember, when solving fractional equations, the process of cross multiplication is utilized.
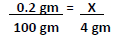   •  → (0.2)(4) = (100)(X) →(0.8) = (100)(X) → X = 0.8 ÷ 100 = 0.008 gm
     
     
3. Therefore, 0.008 gm of hydrocortisone is in 4 gm of a 0.2% hydrocortisone valerate ointment.

Problem 3

You receive the following prescription for a child weighing 20 lb:

What is the day's supply for this prescription?

1. First you must determine the dose in mL. Remember that 1 tsp = 5 ml, therefore the concentration of ranitidine is 75 mg/ 5 ml. This can be done using various methods. For this example, DA will be used.
   
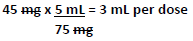
2. Now determine the amount needed per day. The prescription states that the medication is to be given every 12 hours, or two doses per day.
   
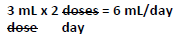
3. Finally, divide the quantity prescribed by the total daily dose
   

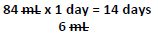
CONCLUSION

Pharmacy technicians spend approximately two-thirds of a typical workday assisting the pharmacist in serving patients, while the remainder of their time is devoted to inventory control and pharmacy practice management.³ Therefore, every technician must be proficient in the use of Roman and Arabic numerals, converting between systems of measurement, computing the day's supply of medications, and working with ratios and proportions. When technicians are competent in these areas, medication errors are less likely to occur because the accuracy of pharmacy calculations is essential to the health and well-being of each patient.

REFERENCES

1. Dussault G, Dubois CA. Human resources for health policies: a critical component in health policies. Hum Resour Health. 2003;1(1):1.
2. Lo A, Co M, Lo C, et al. Specialized pharmacy oncology technician: experience at the Ridge Meadows Hospital. Can J Hosp Pharm. 2010;63(2):138-141.
3. Council on Credentialing in Pharmacy. Albanese NP, Rouse MJ. Scope of contemporary pharmacy practice: roles, responsibilities, and functions of pharmacists and pharmacy technicians. J Am Pharm Assoc (2003). 2010;50(2):e35-e69.
4. Ansel HC, Stoklosa MJ. Pharmaceutical Calculations. 11th ed. Philadelphia, PA: Lippincott Williams &Wilkins; 2001.
5. Kee JL, Marshall SM. Clinical Calculations: With Applications to General and Specialty Areas. 7th ed. St. Louis, MO: Elsevier Saunders; 2013.
6. Zentz LC. Math for Pharmacy Technicians. Sudbury, MA: Jones and Bartlett Publishers, LLC; 2010.
7. Medication Safety Tools and Resources. Institute for Safe Medication Practices website. 2017. http://www.ismp.org/tools/default.aspx. Accessed July 2019.
8. ISMP's list of error-prone abbreviations, symbols, and dose designations. Institute for Safe Medication Practices website. 2015. http://www.ismp.org/tools/errorproneabbreviations.pdf. Accessed July 2019.
9. Pharmacy Auditing and Dispensing Job Aid: Billing Other Dosage Forms. Centers for Medicare and Medicaid Services website. December 2015. https://www.cms.gov/Medicare-Medicaid-Coordination/Fraud- Prevention/Medicaid-Integrity-Education/Downloads/pharmacy-selfaudit-jobaid-billing-other.pdf. Accessed July 2019.

Back to Top